Рекомендации для учителя

На этом уроке продолжим изучать комбинаторику. Ранее мы изучили понятие перестановки. На основе комбинаторного закона умножения сформулировали правило нахождения числа перестановок. На этом уроке мы изучим новое понятие — «сочетания», а также научимся находить число сочетаний.

Проверка знаний и умений учащихся.

Повторите материал прошлого урока путем опроса.

Вопросы:

1. Сформулируйте комбинаторное правило умножения.

Ответ: Чтобы найти число различных упорядоченных пар, составленных из предметов двух типов, нужно число предметов первого типа умножить на число предметов второго типа. Если число предметов первого типа равно m, а число предметов второго типа равно n, то число всевозможных их комбинаций равно mn.

2. Что такое перестановка из n элементов?

Ответ: Перестановкой n элементов называют упорядоченную последовательность чисел, в которой каждое натуральное число от 1 до n встречается ровно один раз.

Или иначе: Перестановкой порядка n называется способ нумерации элементов множества, в котором n элементов.

3. Дайте определение факториалу числа.

Ответ: Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n.

4. Чему по определению равно число 0!?

Ответ: 1.

5. Как найти число перестановок порядка n?

Ответ: n!

Получение новых знаний.

На прошлых уроках нам встречались задачи, в которых речь шла о выборе нескольких предметов из имеющихся. Если речь шла об упорядоченном выборе (выставить несколько книг на полку в определенном порядке), то достаточно было просто применить закон умножения. Когда же порядок не имеет значения, комбинаций меньше. Начните с простого примера.

Пример 1. Маше подарили набор из семи мелков всех цветов радуги. Сколькими способами она может выбрать:

а) два; б) три; в) четыре цвета?

Желательный результат обсуждения. Выбрать по очереди два мелка Маша может 7⋅6=42 способами. Но при этом каждый набор мы считаем два раза: например, пары «красный+зеленый» и «зеленый+красный» (см. рис. 1). Поэтому на самом деле два мелка Маша может выбрать $\frac{42}{2} = 21$ способом.

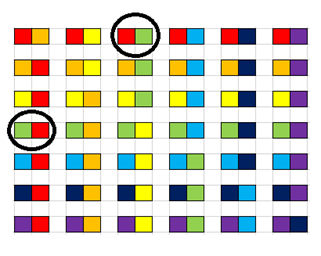Рис. 1

Три мелка Маша может выбрать по очереди 7⋅6⋅5=210 способами, но тут, как и в пункте а), порядок выбора не важен.

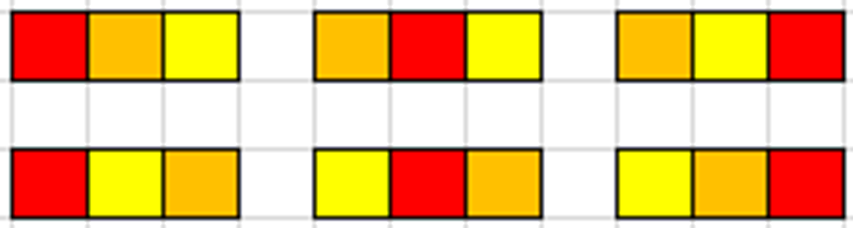Рис. 2

Предложите учащимся подумать над тем, сколько раз мы считаем каждый набор из трех мелков при таком подсчете? Нетрудно догадаться, что три цвета мы можем переставить шестью способами (см. рис. 2), потому как из трех разных цветов мы можем составить ровно 3!=6 перестановок. Поэтому три цвета Маша может выбрать $\frac{210}{6} = 35$ способами.

Выбранные цвета Маша сочетает между собой. Поэтому выбранные комбинации называют сочетаниями. Сочетания могут состоять не только из мелков, но из любых предметов. Часто при решении задач нужно найти количество сочетаний из определенного числа предметов.

Определение. Число способов, которыми можно выбрать ровно k предметов из n предметов, называется числом сочетаний из n по k и обозначается $C_{k}^{n}$ (читается «цэ из эн по ка»).

Таким образом, при решении задачи мы получили, что C 7 2 =21 и $C_{7}^{3} = 35$ .

В пункте в) нужно найти $C_{7}^{4}$ . Предложите учащимся самостоятельно решить задачу для числа сочетаний из четырех мелков, наметив план действий: нужно найти количество способов по очереди выбрать четыре мелка, а потом разделить на количество возможных перестановок этих четырех мелков. В результате получится $\frac{7 \cdot 6 \cdot 5 \cdot 4}{4!} = 35.$

Если школьники заметят, что полученное число совпадает с ответом к предыдущему пункту, можно согласиться с ними, сказать, что это не случайность, и предложить разобраться в этом вопросе самостоятельно либо немного подождать.

Обобщите результат. Если нам нужно выбрать k из имеющихся n предметов, то количество способов это сделать можно найти, разделив количество способов по очереди выбрать k предметов на число перестановок из k выбранных предметов:

$\frac{n \cdot (n - 1) \cdot \dots \cdot (n - k + 1)}{k!}$

Когда в задаче речь идет о неупорядоченном выборе нескольких элементов из имеющихся, учащиеся должны понять, что нужно найти число сочетаний.

Если число n небольшое, то число сочетаний $C_{n}^{k}$ можно взять из треугольной таблицы, которая называется треугольником Паскаля.

Обычно треугольник Паскаля изображают в виде равнобедренного треугольника, как на рис. 3. Треугольник продолжается бесконечно вниз, но изображают только несколько первых строк. Из-за треугольной формы таблицы столбцы в треугольнике получаются наклонные.

Рис. 3. Треугольник Паскаля для n=0,...,10

В каждой строчке содержатся числа сочетаний из n элементов.

$C_{6}^{0}$	$C_{6}^{1}$	$C_{6}^{2}$	$C_{6}^{3}$	$C_{6}^{4}$	$C_{6}^{5}$	$C_{6}^{6}$
1	6	15	20	15	6	1

Эту строку легко найти в треугольнике Паскаля. Она седьмая по счету, но в треугольнике Паскаля строки и столбцы нумеруются с нуля, поэтому лучше считать, что числа сочетаний из 6 находятся в строке с номером 6.

При такой нумерации строк и столбцов число $C_{n}^{k}$ стоит в n-й строке и в k-м столбце (см. рис. 4). Например, чтобы найти $C_{6}^{4}$ , достаточно посмотреть, какое число стоит на пересечении 6-й строки и 4-го столбца: $C_{6}^{4} = 15$ .

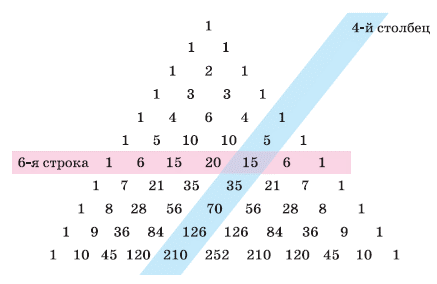Рис. 4. Поиск числа $C_{6}^{4}$ в треугольнике Паскаля

Если число n невелико, то число сочетаний можно просто взять из треугольника Паскаля. Если же n велико, то приходится пользоваться формулой

C_{n}^{k} = \frac{n \cdot (n - 1) \cdot \dots \cdot (n - k + 1)}{k!} .

У этой формулы есть краткая запись: $C_{n}^{k} = \frac{n!}{k! \cdot (n - k)!}$ , но она менее удобна при расчетах.

Потренируйтесь с учащимися в использовании треугольника Паскаля.