Рекомендации для учителя

В математике есть специальный инструмент для изображения и изучения связей между объектами. Это граф. Как числа используются для счета объектов, вне зависимости от их природы, так и граф изображает связи между объектами, вне зависимости от их природы.

На уроке мы познакомимся с тем, как информацию представляют с помощью графов.

Подготовка к активному и сознательному усвоению материала.

Рассмотрите схемы. Что на них изображено? Что общего у этих схем?

 

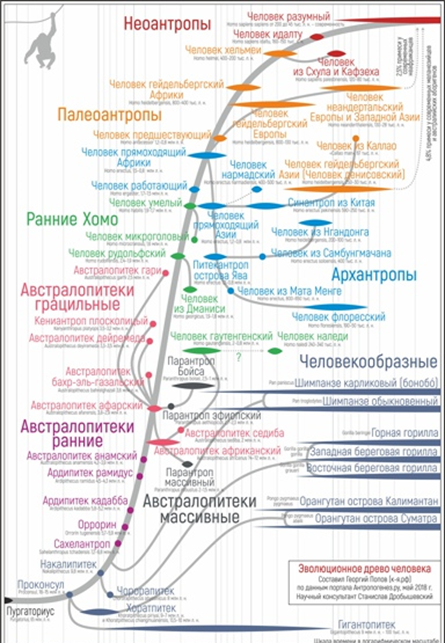
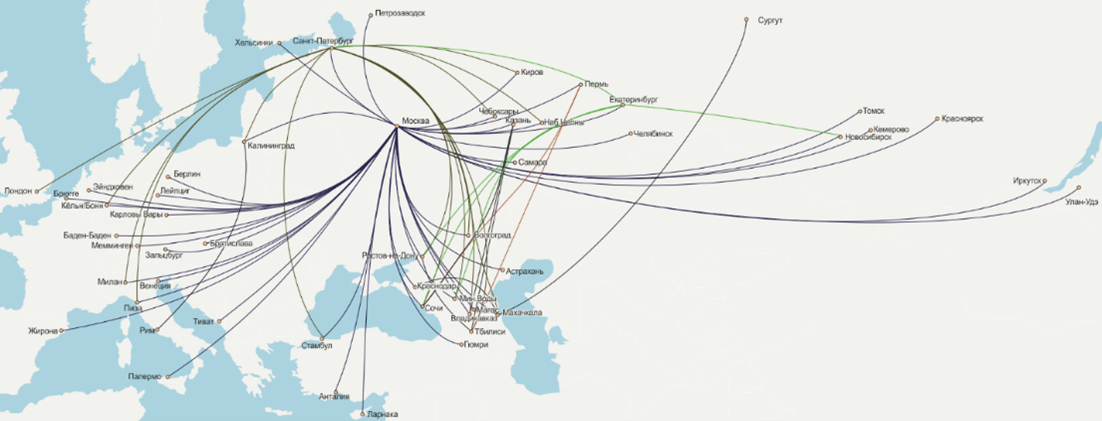
На первом рисунке изображена схема метрополитена г. Санкт-Петербурга; на втором изображено эволюционное древо человека; третий содержит информацию о внутренних перелетах по России некоторой авиакомпании.

На всех трех рисунках изображенные объекты (станции метро, этапы развития человека, города) обозначены точками и эти точки соединены между собой отрезками или дугами, которые отображают связь между этими объектами.

Например, наличие отрезка между Москвой и Петрозаводском на схеме авиарейсов говорит о том, что между этими городами есть прямое авиасообщение. А вот из Иркутска в Сургут не долететь прямым рейсом этой авиакомпании.

Такое представление информации о перелетах имеет очевидное преимущество перед обычной таблицей рейсов.

Мы рассмотрели примеры объектов и связей между ними.

Получение новых знаний

Часто разные объекты удобно изображать точками, а связи между ними — линиями. Такие изображения называются графами.

Точки графа называются вершинами. Некоторые (не обязательно все) вершины соединены линиями, которые называются ребрами.

Примеры графов:

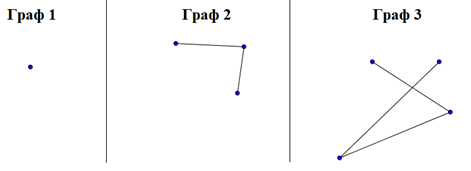Рис. 1. Самый простой граф — точка без ребер (граф слева)

 

У каждого ребра два конца — вершины графа. Если вершина является концом ребра, говорят еще, что ребро исходит из этой вершины, или что оно входит в нее. Вершина не обязательно должна быть соединена ребрами с другими вершинами. Вершину, из которой не выходит ни одно ребро, называют изолированной.

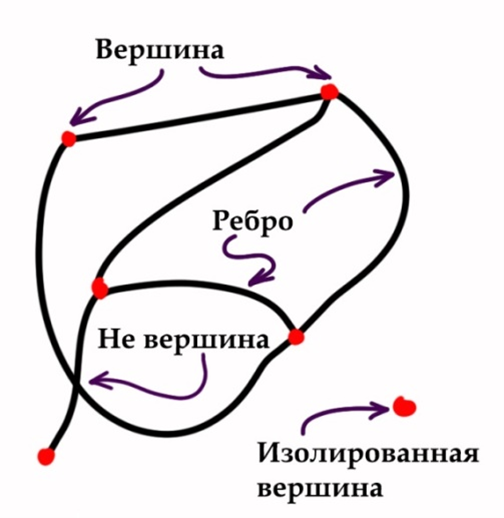Рис. 2

Графы помогают визуально представить взаимосвязь между объектами. Точками обозначаются сами объекты, а ребра отображают парные связи между этими объектами.

Объектами могут быть города, а связями — прямые рейсы между ними. Предложите ученикам самим придумать примеры множеств, связь между элементами которых удобно изобразить в виде графа (схема движения автобуса или любого другого транспорта, схема того, кто с кем дружит в классе, генеалогическое древо и так далее).

 

Как правило, важны только сами вершины и связи между ними; взаимное расположение вершин на рисунке не важно. Можно представлять себе граф как пуговицы, соединенные растяжимыми нитями. Пуговицы можно двигать как угодно, лишь бы нити не рвались и не добавлялись новые.

Каждая вершина должна быть явно отмечена. Иногда ребра на рисунке пересекаются, но точка пересечения не является вершиной графа. Это как две нитки: они могут пересекаться, но узелка в точке пересечения нет.

Одну и ту же систему связей можно изобразить по-разному.

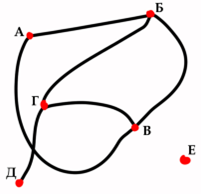Рис. 4

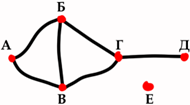Рис. 5

Например, на рисунках 4 и 5 мы видим два одинаковых графа. Здесь все вершины отмечены буквами от А до Е. На обоих рисунках вершина А связана ребрами с вершинами Б и В; вершина Б — с вершинами А, В и Г; В — с А, Б и Г; Г — с Б, В и Д; Д — с Г; а вершина Е не связана ребрами с другими вершинами.